Repaso de propiedades: Potencia y Raíz

Continuamos con el repaso de las operaciones más básicas, sin embargo resultaba prudente para que la información sea fácil de digerir, que la potencia y la raíz recibieran una entrada aparte.

La razón por la cual la potencia es tan importante, trasciende a que el operador se encarga de realizar múltiples productos de manera abreviada, la potencia (y la raíz por contratarte) son esenciales para el estudio del álgebra.

De hecho, el lector o lectora puede advertir que en geometría, el estudio de superficies y volúmenes relaciona distancias 'al cuadrado' y no 'multiplicadas por si mismas'.

La siguiente tabla resume sus propiedades:





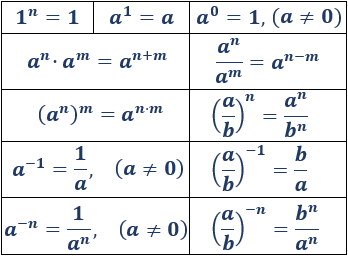
Note como la potencia puede distribuirse en un producto/división, esto es fácilmente comprobable numéricamente, sin embargo un error muy común en los estudiantes de secundaria es la siguiente FALSA suposición:

( a + b )^2  = a^2 + b^2                      Nota: el símbolo ^ refiere a 'elevado a la...`

La suposición de arriba no solo es FALSA, sino que también es muy común

Vea el siguiente ejemplo:
Supongamos que usamos la notación erronea y procedemos a resolver lo siguiente.

( 2 + 1 )^2  = 2^2 + 1^2 = 4 + 1 = 5         
Sin embargo, si procedemos a resolver el enunciado de respetando la prelación de las operaciones, esto quiere decir, resolver lo que está dentro del paréntesis primero.

( 2 + 1 )^2 = 3^2 = 9

Aquí hay una discrepancia, un método dio un resultado y otro dio uno completamente distinto. Sin embargo, en uno de ellos nosotros ejecutamos una 'propiedad' que dimos por valida, mientras que en el otro método, resolvimos de manera ordenada, sin aplicar ninguna propiedad, teorema, nada.
Esta claro que el primer camino es incorrecto ya que la propiedad distributiva de la potencia solo es valida para productos y divisiones, no para sumas y restas



Raíz:

La raíz opera de manera inversa a la potencia, esto quiere decir que mientras en una potencia procedemos a realizar múltiples productos sucesivos, en la raíz nosotros buscamos al numero que cuando se lo eleva al numero que indica la raíz, se obtiene el numero que esta debajo de ella. Dicho de otro modo:


Sobre notacion:
Mencionamos previamente que la potencia y la raíz son intrínsecamente la misma operación, de modo que la raíz es la operación inversa a la potencia y la potencia será la operación inversa a la raíz.
Esto quiere decir que podemos escribirlas de la siguiente manera:

a ^ (b/c)   Aquí, sea (a) un número cualquiera, nos dice que esta elevado a una potencia fraccionaria. La cual se traduce de la siguiente manera. (b) será la potencia a la cual se somete el número (a), y (c) será el índice de la raíz que también afecta al mismo número (a)

Esto nos permite considerar el hecho de que todo número entero puede interpretarse como fraccionario con un 1 en su denominador. Sin embargo nosotros sabemos que un 1 en el denominador es igual a tomar un número y dividirlo por 1, ya vimos que esto no cambia en nada a dicho número (Es el elemento neutro).
Del mismo modo, vemos que todo número elevado a una potencia natural tiene en su denominador un 1, pero un 1 no cambia en nada, es tener una raíz con indice 1, esto no afecta en nada a la operación, es su elemento neutro.

IMPORTANTE:

Si la cantidad subradical (c) es un numero negativo y el índice es un numero par, digamos por ejemplo 2, esto sería pedir que dos números cualquiera se multiplicasen el uno con el otro y que den como resultado un número negativo.

Esto es imposible, recordar como se comportan los signos durante el producto:
 
+ . + = +
- . - = +
+ . - = -
- . + = -

De modo que el producto de dos (o cualquier numero de veces par ) números negativos, siempre será positivo.
Sin embargo, si los multiplicamos un número negativo impar de veces, digamos por ejemplo 3 veces, se obtiene un número negativo.

Conclusión:
( -a )^(1/2)  No existe. Y no existirá nunca, no importa el (a) y la cantidad par del número en el índice.